A powerful and systematic innovation and real life problem solving approach

You would reach a solution much quicker and with assurance if you adopt time-tested and systematic problem solver's approach rather than follow a random personal approach

Journey is more important

When solving a problem, we think usually like others, like normal people. If a problem directly affects us in an emotionally charged situation, we usually lose our capability to think clearly and to evaluate the alternatives with a cool head. These are technically termed as Affective problems. In these sessions of systematic and scientific real life problem solving we won’t generally deal with affective problems in a direct manner.

Selecting a house, planning for a trip, preparing for exam, strategic business policy making – all are real life largely non-affective problems that can be tackled better by adopting systematic problem solver’s approach compared to random trial and error approach.

I won’t say that no one can beat the systematic approaches that we are discussing. I only mean that these systematic (and scientific) real life problem solving approaches, if practiced seriously by anyone, will be of great help in reaching a better solution at a lesser cost in most of the cases.

We already know that not all problems can be solved by a single method. Depending on the type of problem, a suitable problem solving resource needs to be used. As you continue to know the use of various problem solving resources, your general problem solving capability will automatically grow to a point where you will be able to create a new resource (or method) yourself when you face a totally new problem. 

In this session, we will expose you to one of the most powerful approaches to general problem solving, be it personal or be it a workplace problem. We will use an artificial but carefully created well known problem to make our point.

Problem example for elaborating the powerful problem solver's approach

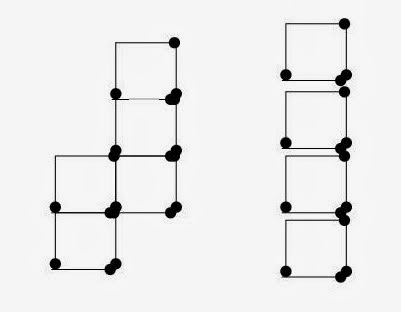
Problem 13.1: First Matchstick problem

You have to move just two matchsticks and reuse these to transform the figure below to four equal squares.

You may spend maximum half an hour’s time to solve the problem. This is a matchstick world and many interesting problem puzzles are available that would challenge your problem solving capability. But we are not here to know the solution, rather our objective is to know how best to reach the solution. Our focus is not on the solution but on the process of arriving at the solution.

Okay, let us take a break here leaving you to solve the problem yourself.

Problem Solution with reasoning:

Usual approach is random trial and error that takes a lot of time and may not be successful. Moreover, if you get the solution this way, you won’t remember how you reached the solution – in short, you cannot reuse the experience of solving the problem.

Then what is the systematic method to solve the problem?

 The approach is to form an idea of the final solution at the initial stage itself and use it intelligently.

To form this Initial Final Solution, we need to analyze the problem first. By initial analysis we conclude: in the final solution no matchstick can be shared between two squares. This is the key discovery and binding condition.

We draw such a possible figure shown below right. This is a possible final solution.

At the next step we will examine this possible solution for suitability. How do we do that? Why did we keep the original figure below left?  

The reason why we kept the original configuration of five squares is: we want to compare the new figure with the original one. The new configuration is no doubt a possible final solution, but we need to judge whether it is the final one. To do this, what do we need to know?

We need to know how much similarity or commonality in structure the figures have. If the new figure has a large portion of the structure common to the original one, changes needed to arrive at the new figure from the old will be that much less.

So, by this logic we can conclude that amongst all the possible final solutions, the ideal final solution will have maximum portion of its structure common to the original configuration. As these figures are pictorial, we can judge commonality by visual inspection only. It should not be a difficult process. The first trial is found to be not a very encouraging one. Let us then see the second possible final configuration.

Still the commonality is not very encouraging. Let us try a third possibility.

Well this is an interesting structure. It has four independent squares utilizing all 16 sticks but also has a lot of commonality with the original structure. Let us assume it as the probable final solution and start trying to transform the original. This is then officially accepted as the Initial Final Solution for the time being.

We see that three squares are exactly same in both the configurations. We then need to destroy two squares in the original and create a new one as blue dotted square in the new configuration. Two sides of square in the new structure already exist. So we just have to move in two more sides and the new square will come to life.

Moving two sticks with arrow points will do just that. We have our final solution.

Now isn’t the method so much fun and easy compared to any other approach? Not only that, if you think a bit, you will understand that this approach can be applied practically in all problems involving matchsticks. You can even create new problems for others to solve. This pattern based initial final solution driven approach makes you a powerful problem solver at least in this kind of problems.

Step by step elaboration of the powerful initial final solution based pattern driven problem solving approach:

Step 1: Analyze the problem and identify the special characteristics of the problem. In our case, this is “in a four square configuration, no two adjacent squares to share a stick, two squares to be destroyed and one new square to be created.”

Step 2: With the knowledge gained in the first step, create as many possible final solutions as you can and test each with our problem condition or criteria. In our case the criterion of comparison is: “to identify the possible final solution satisfying the conditions in Step 1 and also having maximum commonality in structure with original configuration.” Identify the target solution. This is your Initial Final solution.

Step 3: Now examine this final solution with respect to your problem criteria and goals, analyze and identify the steps to reach the goal. In our case we identify the three common squares, the two squares that are to be destroyed and the one new square to be created and finally identify the two sticks to be moved and the place where these are to be moved.

Step 4: Implement the solution and check again to see that the solution satisfies all conditions and indeed your target solution. In our case we actually move the two sticks 7 and 12 to reach the final solution.

It is interesting to note that this approach, though sounds simple is powerful enough to be applied in many problem situations. This of course has to be applied with all techniques, tools and larger methodology that are at your disposal and you find suitable for your problem at hand.  This core approach is supported by both TRIZ and McKinsey approaches in addition to working backwards approach we learned earlier.

In this case we have used the Initial Final Solution approach and also Pattern matching (identification) technique. Pattern matching technique is a generic one and can be applied in a large number of situations with suitable variations.

Here, you must remember, the most important capability is to form the Initial Final Solution based on initial analysis of the problem.

Knowing everything about a problem domain requires lots of time and effort, a single approach, however powerful it is, may not be sufficient to take control of the domain knowledge.

Second problem example to show limitation of one approach in solving all problems in a domain:

Problem 13.2: Second Matchstick problem

You have to convert the following three equal squares made up of matchsticks into four equivalent squares.

Do you have to use any extra matchstick?

If yes, what is the minimum number of extra matchsticks you would need?

Here similarity in structures is not the critical criterion and also instead of matchstick rearrangement, extra matchstick addition is considered. This gives rise to a basic question: how can we be in a position of total knowledge control of the all the domain variability?  The way to do that is to identify exhaustively all the critical variabilities and their combinations. Can we do that? To do this we need to resort to another important principle: the principle of exhaustivity.

If you continue to explore the problem domain even after solving a specific problem, you will gain valuable insights, will form important rules and processes and move towards a position of total control of the domain knowledge. Sometimes that is exciting. One way to explore a problem domain is to try to solve a specific problem in many different ways. How many ways the problem 13.1 can be solved? I know at least one more nearly equally good way to reach the solution. Will you try?

You can sharpen your analytical skills by practicing on matchstick domain problems that are available easily in large varieties in the web.

I remind you once again, our goal was not to reach the solution only. Our actual goal was to reach the solution using an elegant, low cost (in terms of time spent) and repeatable approach.

At least on one occasion I found someone quick enough to download the solution to this popular problem from the web, thus missing the whole point of problem solving exercise altogether.

Journey is more important and not the destination, and by the same token process of solving a real life problem is more important rather than the solution itself. If the process is right automatically you would reach the desired solution.

To me the most crucial learning: the journey is more important, not the destination. In other words, in this case, the process of solving is more important, and not the solution.

If you wish, you may apply this learning to living your life itself.

Read my other blogs on Innovative idea generation and its basic principles and Get smart, get innovative usingTRIZ