Deeper logic analysis - an useful ability for Innovation and Real life Problem Solving

Compound logic analysis techniques

Power of Logic

Logic analysis primarily deals with yes/no variables or questions. The core concept of this approach of limiting the number of final possible outcomes to only two makes this world of yes/no a certain world. To understand the power of this on/off or yes/no world, you just have to consider that the whole of the digital world is built upon the foundation of two valued Boolean variables. We have achieved, amongst many other great gains, a tremendous leap in accuracy in the digital world compared to the analogue world where a continuously changing parameter can have any number of possible values in a continuum.

Thus excited with the digital world of yes/no logic, one might be tempted to assume that answers to all earthly questions can be obtained using pure logic.

Unfortunately, most of the important factors in real life decision making do not adhere to only two possibilities and thus cannot be analyzed or predicted using pure logic. For real life problem solving, one needs to use whatever resources are suitable and available. Till now we were exposed to:

A few basic principles of problem solving, namely,

      Principle of exhaustivity

    Principle of precise definition

    Principle of interleaving

    Principle of zero based problem solving

A few inventive principles of TRIZ, namely,

   Principle of segmentation or breaking down a larger piece into smaller pieces

   Principle of merging or combining similar type of smaller pieces into a larger one

A few powerful techniques of problem solving, namely,

      Pattern identification

    Enumeration

    Abstraction (though abstraction is more than a technique, we may classify it as a principle itself)

    Structuring

   Induction principle (we classify this as a technique because of its less power and abstraction)

      Domain mapping (we have actually used the concept of divisibility and factorization in Mathematics domain to answer the third question in the area dividing sub-domain encountered in the four square problem)

    Logic analysis

We were also exposed to Concept structure as a problem solving resource.

Additionally, we define now Deductive Reasoning as the overall chaining mechanism that binds all the fact gathering, analyses, and decisions from start to end step of a problem solving process.

Logic analysis is only one of the problem solving resources.  

In spite of logic analysis being only one of the problem solving resources, the core concept of yes/no can be used for creating a few other powerful problem solving tools and techniques. We will be exposed to these later.

Let us now delve a little deeper into this interesting area of logic analysis and solve a more complicated logic problem.

Problem 1: Which path would you take? (version 2)

A logician while visiting the South Seas again is at a fork. He needed to know which of the two paths in front of him leads to the village. In this case, he has three willing natives available nearby. But one of them is from a tribe of invariable truth-tellers, another from a tribe of invariable liars and the third from a tribe of random answerer. The logician knows this but does not know which one is the liar, the truth-teller or the random answerer. The natives though know each other well. The logician can ask only two yes-no questions each directed to just one of the natives. Can he know the right path to the village?

Very hard? Well, it seems to be so in the beginning. But remember one golden principle: however difficult and complex a problem seems to be in the beginning, it is bound to get simpler if you can break it up intelligently into smaller pieces. This is called Fragmentation or Problem breakdown principle.

With this hint of a golden principle we will leave you to solve this problem yourself. You can take an hour if you wish, but please do make a serious attempt to solve this problem. Use your deductive reasoning. Analyze and formulate inviolable conclusions.

Solution: Can you break up this problem into two smaller problems? Yes you can. If you observe closely, you will find that the last question situation must exactly be like the version 1 of the problem, that is, one question, two alternatives and two natives (or one native)– the liar and (or) the truth teller left. This is because, at the last stage, if the random answerer is left and you put the common question to the random answerer his answer may be yes or no, whereas at the last stage you must get one specific answer to your specific common question. Thus the problem is transformed and reduced to the form,

First question, three natives, objective: eliminate the random answerer.

Notice that here also you have used your deductive reasoning capability.

How can you meet the objective of eliminating the random answerer at the first step?

Consider: in the second question, you have to ask the question involving the right path, otherwise you won’t be able to know the right path; that is a certainty. In the case of the first question would you ask about the right path? Is it reasonable? It is not. Instead you must ask about the answering nature of the natives.  You will form the question in such a way that when you ask the second question the troublesome and unpredictable random answerer is no longer there.

What should be the first question?

Asking a native about his own nature will not lead you anywhere. So you must ask a native about the nature of the other two natives.

What can be the type of question?

A new technique is to be used: pair-wise comparison is a powerful technique for reliable comparison.

Let us now use the technique of enumeration. We assume scenarios of nature of the natives and then analyze the possibilities arising in each scenario.

Comparison regarding reliability of answer: Truth teller vs. random answerer: What conclusion can you draw?

Truth teller answers truthfully all the time, whereas random answerer answers truthfully 50% of the time. So, Truth teller is more likely to answer truthfully compared to the random answerer. Oh yes, the phrase “More likely” is the key. This is Testing & information discovery. With this knowledge now we would enumerate the scenarios and continue our analysis.

Scenario 1: You ask the first question regarding reliability of answer to the liar (C) comparing the answering nature of the truth teller (A) and the random answerer (B). This is a clear application of Enumeration.

In this specific case, the liar will answer NO, but if nature of A and B are reversed, answer will be YES.

This knowledge leads to the decision: If the answer to the first question regarding comparing the answering nature of two other natives is NO, ask the second question to A, if it is YES ask the second question to B (in both cases you will then ask the second question to the truth teller, eliminating the random answerer).

Scenario 2: Comparison between Liar (A) and random answerer (B). Question to C, the truth teller.

In this specific case, true answer is NO (Liar A is not more likely to answer truthfully than random answerer B), and as C is truth teller his answer will still be NO. If nature of A and B are reversed, answer will be YES.

This result leads you to the decision: If this answer is NO, ask the second question to A, if it is YES, ask the second question to B (in both cases you will then ask the second question to the liar, thus eliminating the random answerer).

What a surprise! In both the scenarios you have asked the same question and got the same desired outcome. In the desired outcome, either liar or the truth teller is left for facing the already known second question. Random answerer is eliminated.

You now ask the question of version 1 of the problem to any one of truth teller or liar left and will surely come to know the right path (as per version 1 of problem). But what if the first question goes to the random answer, marked here as C?

Scenario 3: If the first question goes to C, the random answerer, B and C are either the liar or the truth teller and your promising first question still holds right. That simple!

Let us now analyze your problem solving process. Remember: solving a problem is not enough; to understand and reuse the process of solution, you must analyze and clarify the problem solving process.

Analysis of problem solving process:

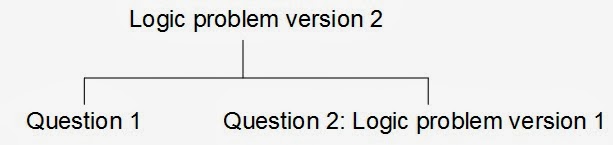
First you have used problem breakdown principle identifying that when the second question is asked, the situation must be similar to version 1 of the problem for you to get the right answer. This is somewhat like the figure below.

Note that, as you already know how to solve the version 1 of the problem, it has become easier for you to solve the problem version 2. What exactly did you know about the version 1 problem? You knew the problem description, problem modelling and process of reaching the solution. In short you have in your mind the concept structure for the version 1 of the problem. This is a clear example of using a concept structure in which you have used the concept structure of problem version 1 in solving the problem version 2.

What is the use of a concept structure in general? All knowledge is held in our mind in the form of concepts that are linked together in the form of concept structures. There are various forms of structures that we can use for representing the relationships between the concepts in a problem.

To formulate the first question then, you have used the techniques of Testing & Information discovery. You have discovered “more likely” as the key phrase in your first question.

Now is the time of enumeration. You have enumerated two scenarios and homed into the same promising form of question and action plan related to the answer.

Can you form the final form of the first question now?

I will leave you here to the pleasant experience of reaching the solution at last, after the seemingly interminable collection of statements.

Read my other blogs on Innovative idea generation and its basic principles and Get smart, get innovative usingTRIZ